Calculating phenology and collated indices with rbms
From counts to flight curve to collated indices
Reto Schmucki (UKCEH) & Dylan Carbone
23rd of July 2024
Source:vignettes/vignette.Rmd
vignette.RmdThe rbms package allows users to derive species
phenology and estimate abundances of butterfly species. In this
tutorial, we use R functions implemented in the rbms
package to produce the following key outputs:
- Compute a flight curve: A spline fitted curve, representing the activity of the species within the monitoring season. The flight curve computation is based on a spline fitted on the counts collected across multiple sites and standardised to sum to 1 (area under the curve is one).
- Site indices and annual collated indices: The yearly abundance at each site, and a model estimate of yearly abundance across all sites.
Pre-requisite steps include the construction of a time series and imputation of counts from the flight curve when abundance data is missing.
The data used in this vignette are bundled within the package and are from genuine Butterfly Monitoring Scheme surveys.
1. Setup
First, install and load required packages.
# Install required packages
install.packages("remotes") # To install R packages from github## Installing package into 'C:/Users/retoschm/AppData/Local/Temp/Rtmp8KZU6U/temp_libpath4570d72b51'
## (as 'lib' is unspecified)## package 'remotes' successfully unpacked and MD5 sums checked
##
## The downloaded binary packages are in
## C:\Users\retoschm\AppData\Local\Temp\RtmpIdddvC\downloaded_packages
install.packages("ggplot2") # to generate plots in this tutorial## Installing package into 'C:/Users/retoschm/AppData/Local/Temp/Rtmp8KZU6U/temp_libpath4570d72b51'
## (as 'lib' is unspecified)## package 'ggplot2' successfully unpacked and MD5 sums checked
##
## The downloaded binary packages are in
## C:\Users\retoschm\AppData\Local\Temp\RtmpIdddvC\downloaded_packages
# Install rbms from github
# remotes::install_github("https://github.com/RetoSchmucki/rbms.git")
# Load rbms and ggplot2
library(rbms)## Welcome to rbms, version 1.1.3
## This package has been tested, but is still in active development and feedbacks are welcome
## https://github.com/RetoSchmucki/rbms/issues## Warning: package 'ggplot2' was built under R version 4.4.1Then load the bundled butterfly monitoring scheme data bundled with the rbms package.
The header names of the visit and count data need to be consistent, and all columns present in the data loaded for this tutorial need to be present in your data for the functions to work.
Visit data represents the date at which each monitoring site was visited. If no butterfly was observed during a visit, the abundance for that specific visit would be set to zero. This allows to subset positive non-zero counts from the count data set, which result in smaller objects to handle. The visit data may contain many columns, but only two are essential for the function.
NOTE: Visit and count data are provided in data.table format, and likewise data.table syntax is used for many of the data processing steps in this tutorial. Whilst other formats and packages are acceptable, it is recommended for larger datasets that you continue to use data.table, as it is efficient for handling large data sets
- SITE_ID (can be numbers of characters and treated as a non-numeric factor)
- DATE (by default, the format is “%Y-%m-%d” (e.g., 2019-11-28]). If a different format needs to be specified, use the argument DateFormat)
## SITE_ID DATE
## <int> <char>
## 1: 1 2000-04-07
## 2: 1 2000-04-19
## 3: 1 2000-05-12
## 4: 1 2000-05-15
## 5: 1 2000-05-24
## ---
## 12136: 193 2004-08-19
## 12137: 193 2004-08-31
## 12138: 193 2004-09-04
## 12139: 193 2004-09-15
## 12140: 193 2004-09-28Count data must be provided in columns with specific headers; more column can be provided, but rbms only use the following four:
- SITE_ID
- DATE
- SPECIES
- COUNT
## SITE_ID DATE SPECIES DAY MONTH YEAR COUNT
## <int> <char> <int> <int> <int> <int> <int>
## 1: 1 2000-04-07 2 7 4 2000 5
## 2: 1 2000-04-19 2 19 4 2000 3
## 3: 1 2000-05-12 2 12 5 2000 1
## 4: 1 2000-05-12 4 12 5 2000 2
## 5: 1 2000-05-15 4 15 5 2000 4
## ---
## 5303: 193 2003-09-06 2 6 9 2003 1
## 5304: 193 2004-04-23 2 23 4 2004 2
## 5305: 193 2004-05-02 2 2 5 2004 1
## 5306: 193 2004-06-19 2 19 6 2004 2
## 5307: 193 2004-07-10 2 10 7 2004 12. organise the data to cover the time period and monitoring season of the BMS
Using the visit and count data, we need to create a new data.table object representing a time series. We initialise the time-series, specifying the start and end year of the monitoring season, with entries at a weekly or daily basis (the resolution of the flight curve). In a first step, we initialise the time-series with an initial year with the InitYear argument, and end year with the LastYear argument. We also specify the first day of the week with the WeekDay1 argument as either ‘sunday’ or ‘monday’.
2.1. First, we initialise a time-series with day-week-month-year information.
ts_date <- rbms::ts_dwmy_table(InitYear = 2000, LastYear = 2003, WeekDay1 = 'monday')2.2. Add the monitoring season to the time-series
We build upon the time series with the monitoring season, providing
the StartMonth and EndMonth arguments. The definition of the monitoring
season can be refined with more arguments of the start and end date
(StartDay, EndDay). We also define the resolution of the time-series as
weekly using the Timeunit argument (w or d for
weekly or daily records). The ANCHOR argument adds zeros before and
after the monitoring season, to ensure that the flight curve starts and
ends at zero.
NOTE: For species with overwintering adult and early counts, having an Anchor set to zero might sound wrong, and we are currently working on finding an alternative for these cases to represent the flight curve of those species better.
ts_season <- rbms::ts_monit_season(ts_date, StartMonth = 4, EndMonth = 9, StartDay = 1, EndDay = NULL, CompltSeason = TRUE, Anchor = TRUE, AnchorLength = 2, AnchorLag = 2, TimeUnit = 'w')2.3. Add site visits to the time-series
Now that the monitoring season has been defined, we use the
ts_monit_site() function to integrate the time-series with
the site visits. We use the visit data and link it with the time series
contained in ts_season object.
ts_season_visit <- rbms::ts_monit_site(ts_season, m_visit)2.4. Add observed count
The time-series is next integrated with the count data. Here we must specify the focus species in the sp argument, providing either an integer (we have used 2 here), or a string.
ts_season_count <- rbms::ts_monit_count_site(ts_season_visit, m_count, sp = 2)The resulting data.table object contains zeros and
positive counts recorded along each BMS transects for species 2, over
the entire time-series, but only within the focal monitoring season.
When the counts are missing because the site was not visited, the count
is informed as NA.
## Key: <DATE, SITE_ID>
## Index: <ANCHOR__M_SEASON>
## M_YEAR DATE DAY_SINCE YEAR MONTH DAY WEEK WEEK_SINCE WEEK_DAY
## <fctr> <IDat> <int> <int> <int> <int> <int> <num> <num>
## 1: 2000 2000-01-01 1 2000 1 1 52 1 6
## 2: 2000 2000-01-01 1 2000 1 1 52 1 6
## 3: 2000 2000-01-01 1 2000 1 1 52 1 6
## 4: 2000 2000-01-01 1 2000 1 1 52 1 6
## 5: 2000 2000-01-01 1 2000 1 1 52 1 6
## ---
## 173496: 2003 2003-12-31 1461 2003 12 31 1 210 3
## 173497: 2003 2003-12-31 1461 2003 12 31 1 210 3
## 173498: 2003 2003-12-31 1461 2003 12 31 1 210 3
## 173499: 2003 2003-12-31 1461 2003 12 31 1 210 3
## 173500: 2003 2003-12-31 1461 2003 12 31 1 210 3
## M_SEASON COMPLT_SEASON ANCHOR COUNT SITE_ID SPECIES
## <num> <int> <int> <int> <int> <num>
## 1: 0 1 0 NA 1 2
## 2: 0 1 0 NA 2 2
## 3: 0 1 0 NA 3 2
## 4: 0 1 0 NA 4 2
## 5: 0 1 0 NA 6 2
## ---
## 173496: 0 1 0 NA 184 2
## 173497: 0 1 0 NA 185 2
## 173498: 0 1 0 NA 186 2
## 173499: 0 1 0 NA 187 2
## 173500: 0 1 0 NA 193 23. Compute the yearly flight curve for the data
With the time season data prepared and saved under ts_season_count, can compute the flight curve, representing the species phenology.
we can compute the flight curve for each year by using the
flight_curve function. First we want to impose some minimal
threshold to control the quality of the data used to inform this model.
This is done by setting the Minimum number of visits (MinNbrVisit), the
minimum number of occurrences (MinOccur) and the number of sites
(MinNbrSite) to use to fit the model. These values can influence the
model, and its sensitivity will depend on the species and the dataset.
Still, as a minimum requirement, MinOccur should be set >= 2, the
MinNbrVisit > MinOccur and MinNbrSite >= 5. These thresholds
affect the data that inform your model and the resulting flight curve.
When higher values are chosen, fewer sites will be available and if
insufficient, the thresholds need to be revised.
NOTE: The flight_curve function assumes that species
phenology is the same across sites. The sample size of the data must be
large enough to calculate the flight_curve
You will also have to define some parameters for the distribution for the GAM model as well as the maximum number of times to try to fit the model and the number of samples to use. The later will take a random sample from the data set if it contains more sites than the number specified.
ts_flight_curve <- rbms::flight_curve(ts_season_count, NbrSample = 300, MinVisit = 5, MinOccur = 3, MinNbrSite = 5, MaxTrial = 4, GamFamily = 'nb', SpeedGam = FALSE, CompltSeason = TRUE, SelectYear = NULL, TimeUnit = 'w')## Fitting the flight curve spline for species 2 and year 2000 with 76 sites, using gam() : 2024-08-20 15:07:17.913829 -> trial 1## Fitting the flight curve spline for species 2 and year 2001 with 76 sites, using gam() : 2024-08-20 15:07:19.152067 -> trial 1## Fitting the flight curve spline for species 2 and year 2002 with 87 sites, using gam() : 2024-08-20 15:07:19.660446 -> trial 1## Fitting the flight curve spline for species 2 and year 2003 with 103 sites, using gam() : 2024-08-20 15:07:20.654046 -> trial 1We are given a list of 3 elements as an output of the
flight_curve() function:
- pheno: The standardised phenology curve derived by fitting a GAM model, with a cubic spline to the count data;
- model: The result of the fitted GAM model;
- data: The data used to fit the GAM model.
We can now extract the pheno object, a data.frame that contains the shape of the annual flight curves, standardised to sum to 1. The flight-curves contained in the pheno object can be visualised with the following line of codes.
## Extract the phenology output
pheno <- ts_flight_curve$pheno
# Determine if 'trimWEEKNO' exists and set the appropriate x-axis variable
x_var <- if("trimWEEKNO" %in% names(pheno)){"trimWEEKNO"} else {"trimDAYNO"}
# Create the ggplot
ggplot(pheno, aes(x = .data[[x_var]], y = NM, color = factor(M_YEAR))) +
geom_line() +
scale_color_discrete(name = "Year") +
labs(x = ifelse(x_var == "trimWEEKNO", "Monitoring Week", "Monitoring Day"),
y = "Relative Abundance") +
theme_minimal() +
theme(legend.position = "top")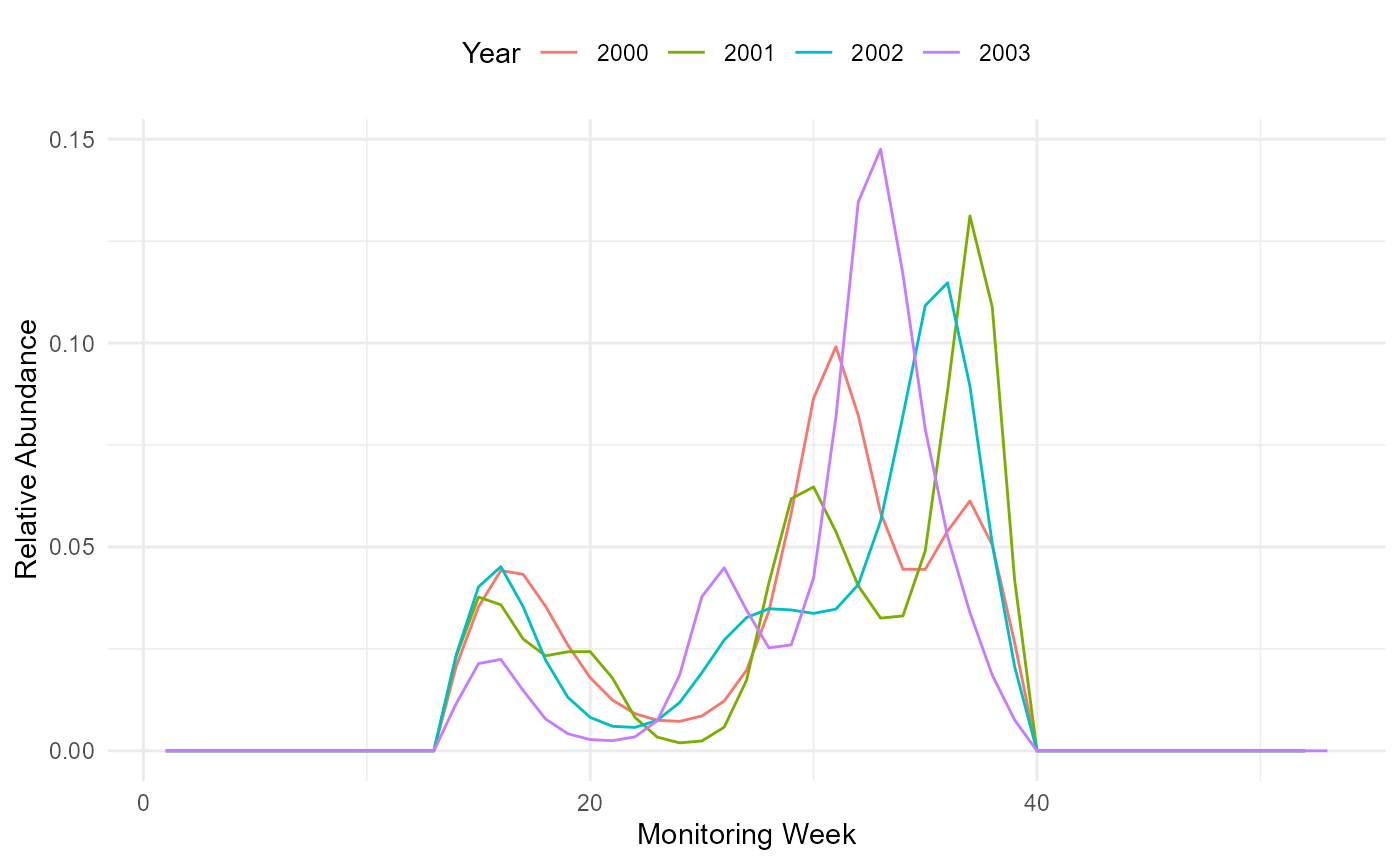
Flight curve.
4. Impute predicted counts for missing monitoring dates
From the flight curve and the observed counts, we can derive expected values for weeks or days where a site has not been monitored. Together, observed and imputed counts are used to compute abundance indices across sites. Site indices are then used to calculate annual collated indices.
The impute_count() function uses the time season data
prepared and saved under ts_season_count, and the flight curves in the
pheno output of the flight_curve() function. The
impute_count() function looks for the phenology available
(using the nearest year) to estimate and input missing values. The
extent of the search for nearest phenology can be limited by setting the
YearLimit argument. By default, this is not restricted and will look
over all years available.
# Impute the count estimates
# Note that the pheno element is extracted automatically from the ts_flight_curve object
impt_counts <- rbms::impute_count(ts_season_count=ts_season_count, ts_flight_curve=ts_flight_curve, YearLimit= NULL, TimeUnit='w')The impute_count() function produces a data.table that
includes the following columns: COUNT: The original count values.
IMPUTED_COUNT: An estimate of the count in the event that there is no
recording of count (I.E., the original count is NA). The imputed count
is derived from the flight curve. If the original count is present, the
imputed count is set as equal to the original count. TOTAL_COUNT: The
sum of the Imputed count within the site and year. SINDEX: The sum of
the imputed counts over the sampling season. If the flight curve of a
specific year is missing, the impute_count() function uses
the nearest phenology found. If none are available within the limit of
years set by the YearLimit argument, the function will return no SINDEX
for that specific year. TOTAL_NM: The proportion of the flight curve
covered by the visits. This is the total count divided by the site
index.
impt_counts_1year <- rbms::impute_count(ts_season_count=ts_season_count, ts_flight_curve=pheno[M_YEAR != 2001, ], YearLimit= 1, TimeUnit='w')## Warning in FUN(X[[i]], ...): We used the flight curve of 2000 to compute
## abundance indices for year 2001
impt_counts_0year <- rbms::impute_count(ts_season_count=ts_season_count, ts_flight_curve=pheno[M_YEAR != 2001, ], YearLimit= 0, TimeUnit='w')## No reliable flight curve available within a 0 year horizon of 20015. Site and collated indices
From the imputed counts, the site_index function can be
used to calculate site index for each year and site. Only sites that
exceed a threshold for the proportional representation of the flight
curve are included. This threshold is set using the MinFC argument,
which In this example is 0.10.
sindex <- rbms::site_index(butterfly_count = impt_counts, MinFC = 0.10)From the site indices, estimates of the annual collated indices are
made using the collated_index() function. Collated indices
represents the mean total butterfly count expected on a BMS transect in
a given year. The function fits a Generalised Linear Model (GLM) with
site and years included as factorial independent variables. The
proportion of the flight curve is included as a GLM weight. When the
argument rm_zero is set to TRUE, all sites where the species are not
observed are filtered, speeding up the fit of the GLM without altering
the output.
co_index <- collated_index(data = sindex, s_sp = 2, sindex_value = "SINDEX", glm_weights = TRUE, rm_zero = TRUE)
co_index## $col_index
## Key: <M_YEAR>
## BOOTi M_YEAR NSITE NSITE_B NSITE_OBS COL_INDEX
## <num> <num> <int> <int> <int> <num>
## 1: 0 2000 124 124 107 18.22935
## 2: 0 2001 108 108 100 30.15065
## 3: 0 2002 114 114 107 30.66658
## 4: 0 2003 122 122 113 59.78319
##
## $site_id
## [1] "1" "14" "157" "158" "159" "160" "161" "162" "163" "164" "165" "166"
## [13] "15" "167" "168" "169" "170" "171" "172" "173" "174" "175" "176" "16"
## [25] "177" "178" "179" "185" "193" "51" "82" "31" "41" "154" "19" "180"
## [37] "181" "182" "187" "183" "184" "186" "21" "23" "24" "25" "26" "27"
## [49] "2" "28" "29" "30" "32" "34" "36" "37" "39" "42" "43" "3"
## [61] "45" "47" "48" "54" "60" "61" "62" "64" "65" "69" "4" "71"
## [73] "72" "76" "83" "84" "85" "86" "89" "91" "92" "6" "93" "95"
## [85] "96" "97" "99" "100" "101" "102" "104" "106" "8" "107" "111" "112"
## [97] "113" "115" "116" "117" "118" "119" "120" "9" "122" "123" "124" "126"
## [109] "127" "128" "129" "130" "132" "133" "10" "134" "135" "136" "137" "139"
## [121] "140" "141" "142" "143" "144" "12" "145" "146" "147" "148" "149" "150"
## [133] "151" "153" "155" "156"The index can be transformed to a log(10) scale.
co_index <- co_index$col_index
co_index_b <- co_index[COL_INDEX > 0.0001 & COL_INDEX < 100000, ]
co_index_logInd <- co_index_b[BOOTi == 0, .(M_YEAR, COL_INDEX)][, log(COL_INDEX)/log(10), by = M_YEAR][, mean_logInd := mean(V1)]
## merge the mean log index with the full bootstrap dataset
data.table::setnames(co_index_logInd, "V1", "logInd"); data.table::setkey(co_index_logInd, M_YEAR); data.table::setkey(co_index_b, M_YEAR)
co_index_b <- merge(co_index_b, co_index_logInd, all.x = TRUE)The log scaled indices can be plotted. Here, we represent the data
with time-series average being centered to two
(i.e. log10(100)) as the standard for British time series
reporting.
col_pal <- c("cyan4", "orange", "orangered2")
## compute the metric used for the graph of the Collated Log-Index centred around 2 (observed, bootstrap sample, credible confidence interval, linear trend)
b1 <- data.table::data.table(M_YEAR = co_index_b$M_YEAR, LCI = 2 + co_index_b$logInd - co_index_b$mean_logInd)
b2 <- data.table::data.table(M_YEAR = co_index_b[BOOTi == 0, M_YEAR], LCI= 2 + co_index_b[BOOTi == 0, logInd] - co_index_b[BOOTi == 0, mean_logInd])
lm_mod <- try(lm(LCI ~ M_YEAR, data = b2), silent=TRUE)
# Create the initial plot with ggplot
p <- ggplot(b2, aes(x = M_YEAR)) +
# Adding the shaded area with white fill
geom_rect(aes(xmin = -Inf, xmax = Inf, ymin = -Inf, ymax = Inf),
fill = "white", alpha = 0.2) +
# Adding the lines and points for non-missing LCI values
geom_line(data = subset(b2, !is.na(LCI)), aes(y = LCI), linetype = "dashed", color = "grey70") +
geom_line(aes(y = LCI), size = 1.3, color = col_pal[1]) +
geom_point(data = subset(b2, !is.na(LCI)), aes(y = LCI), color = col_pal[1], shape = 19) +
# Adding the horizontal line
geom_hline(yintercept = 2, linetype = "dashed") +
# Adding labels and customizing axes
labs(x = "year", y = expression('log '[10]*' Collated Index')) +
scale_x_continuous(breaks = b2$M_YEAR) +
theme_minimal() +
# Making the y-axis appear as a black line
theme(axis.line.y = element_line(color = "black"))## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.
# Adding the regression line if lm_mod is not a try-error
if (class(lm_mod)[1] != "try-error") {
p <- p + geom_line(aes(y = as.numeric(predict(lm_mod, newdata = b2, type = "response"))), color = "maroon4", size = 1.5, linetype = "solid")
}
# show the plot
print(p)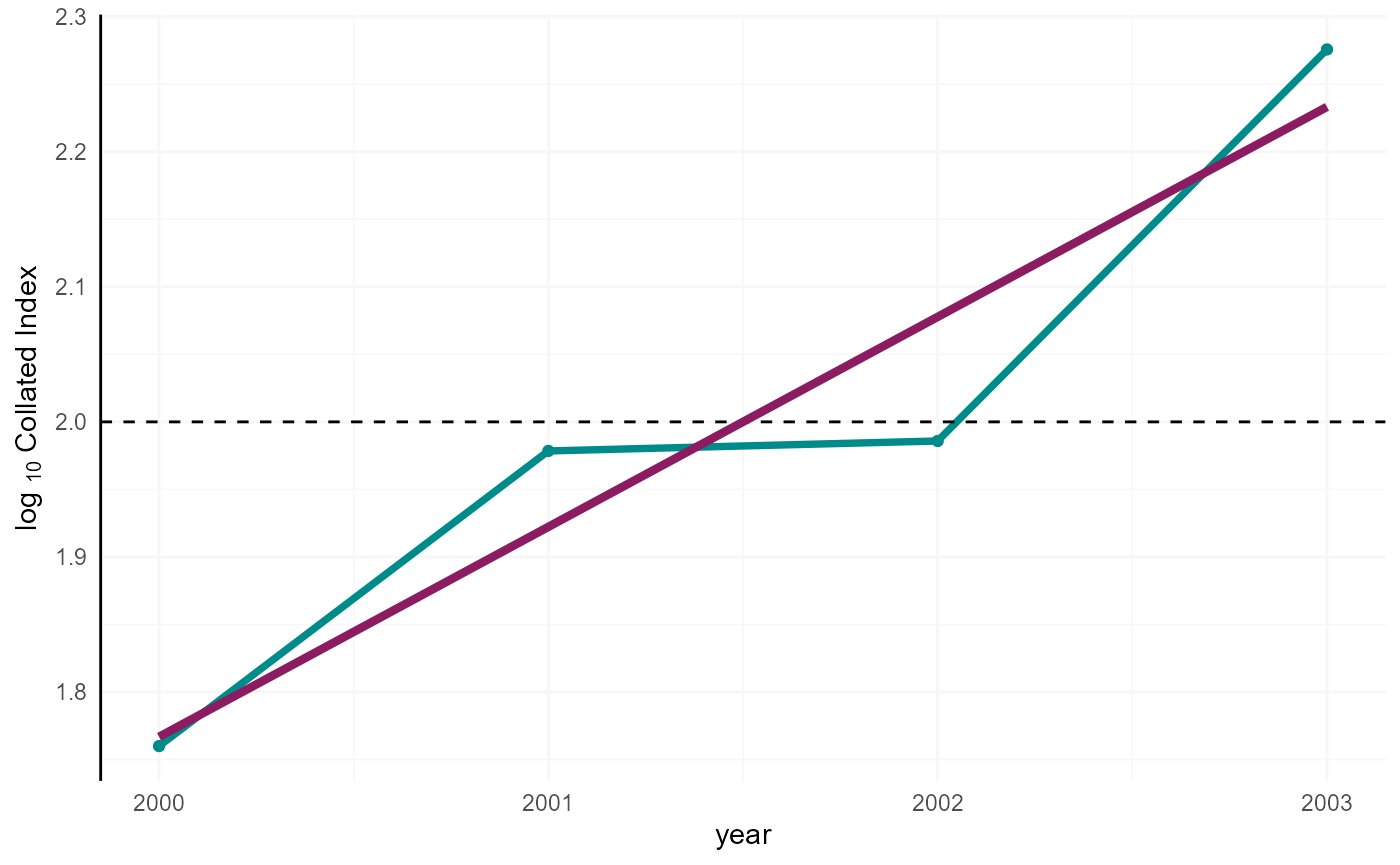
Collated index.
6. Bootstrap confidence interval
the boot_sample() function can be used to compute a
confidence interval around the collated indices. A number of sites are
sampled (randomely, with resampling) a number of times, specified by the
argument, boot_n. This produces a distribution of the annual collated
indices, from which we can can derive the confidence intervals around
the collated indices. In this example, we set boot_n. to 200 samples,
but for a reliable confidence interval, k should be at least 1000. For
reproducibility, we use set.seed() to generate a repeatable random
sample
NOTE: You should not take large numbers of bootstraps from a dataset with a small number of sites, as resampling sites will not introduce new variance.
set.seed(218795)
bootsample <- rbms::boot_sample(sindex, boot_n = 200)Using the collated_index() function in a loop, with
bootstrap samples informing the argument boot_ind, we can
now compute the boot_n number of collated indices over the entire
time-series.
co_index <- list()
for(i in c(0,seq_len(dim(bootsample$boot_ind)[1]))){
co_index[[i+1]] <- rbms::collated_index(data = sindex, s_sp = 2, sindex_value = "SINDEX", bootID=i, boot_ind= bootsample, glm_weights=TRUE, rm_zero=TRUE)
}
# collate and append the results
co_index <- data.table::rbindlist(lapply(co_index, FUN = "[[","col_index"))Annual log indices, as well as their average, are then computed from the original sample. To derive confidence intervals, we compute annual log indices for each bootstrap sample.
co_index_b <- co_index[COL_INDEX > 0.0001 & COL_INDEX < 100000, ]
co_index_logInd <- co_index_b[BOOTi == 0, .(M_YEAR, COL_INDEX)][, log(COL_INDEX)/log(10), by = M_YEAR][, mean_logInd := mean(V1)]
## merge the mean log index with the full bootstrap dataset
data.table::setnames(co_index_logInd, "V1", "logInd"); data.table::setkey(co_index_logInd, M_YEAR); data.table::setkey(co_index_b, M_YEAR)
co_index_b <- merge(co_index_b, co_index_logInd, all.x = TRUE)
data.table::setkey(co_index_b, BOOTi, M_YEAR)
co_index_b[ , boot_logInd := log(COL_INDEX)/log(10)]From the bootstrap samples, we can derive a 95% Confidence Interval, using the corresponding percentiles (i.e., 0.025 and 0.975).
b1 <- data.table::data.table(M_YEAR = co_index_b$M_YEAR, LCI = 2 + co_index_b$boot_logInd - co_index_b$mean_logInd)
b2 <- data.table::data.table(M_YEAR = co_index_b[BOOTi == 0, M_YEAR], LCI= 2 + co_index_b[BOOTi == 0, logInd] - co_index_b[BOOTi == 0, mean_logInd])
b5 <- b1[co_index_b$BOOTi != 0, quantile(LCI, 0.025, na.rm = TRUE), by = M_YEAR]
b6 <- b1[co_index_b$BOOTi != 0, quantile(LCI, 0.975, na.rm = TRUE), by = M_YEAR]
lm_mod <- try(lm(LCI ~ M_YEAR, data = b2), silent=TRUE)
## define graph axis limits and color scheme
yl <- c(floor(min(b5$V1, na.rm=TRUE)), ceiling(max(b6$V1, na.rm=TRUE)))
col_pal <- c("cyan4", "orange", "orangered2")
# Convert b5 and b6 to data frames for easier handling in ggplot
b5_df <- data.frame(x0 = as.numeric(unlist(b5[,1])), y0 = as.numeric(unlist(b5[,2])))
b6_df <- data.frame(x1 = as.numeric(unlist(b6[,1])), y1 = as.numeric(unlist(b6[,2])))
# Combine b5 and b6 into a single data frame
segments_df <- cbind(b5_df, b6_df)
library(ggplot2)
# Convert b5 and b6 to data frames for easier handling in ggplot
b5_df <- data.frame(x0 = as.numeric(unlist(b5[,1])), y0 = as.numeric(unlist(b5[,2])))
b6_df <- data.frame(x1 = as.numeric(unlist(b6[,1])), y1 = as.numeric(unlist(b6[,2])))
# Combine b5 and b6 into a single data frame
segments_df <- cbind(b5_df, b6_df)
# Create the initial plot with ggplot
p <- ggplot(b2, aes(x = M_YEAR)) +
# Adding the shaded area with white fill
geom_rect(aes(xmin = -Inf, xmax = Inf, ymin = -Inf, ymax = Inf),
fill = "white", alpha = 0.2) +
# Adding the segments
geom_segment(data = segments_df, aes(x = x0, y = y0, xend = x1, yend = y1),
color = col_pal[2], size = 2) +
# Adding the lines and points for non-missing LCI values
geom_line(data = subset(b2, !is.na(LCI)), aes(y = LCI), linetype = "dashed", color = "grey70") +
geom_line(aes(y = LCI), size = 1.3, color = col_pal[1]) +
geom_point(data = subset(b2, !is.na(LCI)), aes(y = LCI), color = col_pal[1], shape = 19) +
# Adding the horizontal line
geom_hline(yintercept = 2, linetype = "dashed") +
# Adding labels and customizing axes
labs(x = "year", y = expression('log '[10]*' Collated Index')) +
scale_x_continuous(breaks = b2$M_YEAR) +
coord_cartesian(ylim = yl) +
theme_minimal() +
# Making the y-axis appear as a black line and setting the background color to white
theme(
panel.background = element_rect(fill = "white", color = "black"),
axis.line.y = element_line(color = "black")
)
# Adding the regression line if lm_mod is not a try-error
if (class(lm_mod)[1] != "try-error") {
p <- p + geom_line(aes(y = as.numeric(predict(lm_mod, newdata = b2, type = "response"))), color = "maroon4", size = 1.5, linetype = "solid")
}
# Print the plot
print(p)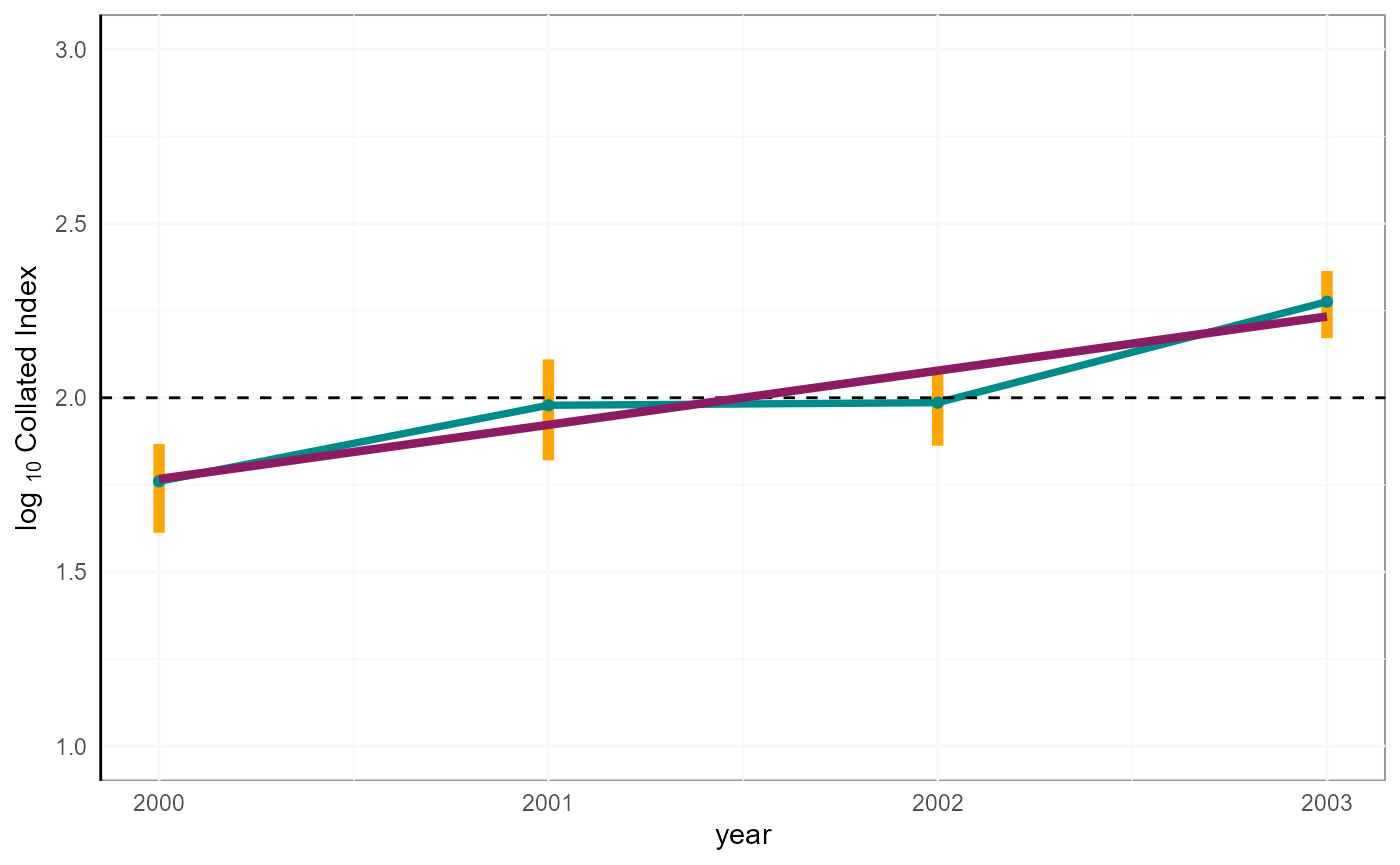
Collated index with 95% CI.